|

|

|
|
The Radon transform
on Z2k
Persi W. Diaconis and Ronald Lewis Graham |
|
Vol. 118 (1985), No. 2, 323–345
|
Abstract |
|
Suppose G is a finite group and f is a function mapping G into the set of real numbers R. For a subset S ⊆ G, define the Radon transform FS off mapping G into R by: 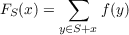 where S + x denotes the set {s + x : s ∈ S}. Thus, the Radon transform can be thought of as a way of replacing f by a “smeared out” version of f. This form of the transform represents a simplified model of the kind of averaging which occurs in certain applied settings, such as various types of tomography and recent statistical averaging techniques. A fundamental question which arises in connection with the Radon transform is whether or not it is possible to invert it, i.e., whether one can recover (in principle) the function f from knowledge of FS. In this paper we investigate this problem in detail for several special classes of groups, including the group of binary n-tuples under modulo 2 addition. |
Mathematical Subject Classification 2000
Primary: 44A15
Secondary: 92A07
|
Milestones
Received: 24 September 1984
Published: 1 June 1985
|
Authors |
| Persi W. Diaconis | |
| Department of Mathematics Stanford University Stanford CA 94305-4065 United States |
|
| Ronald Lewis Graham | |
 |
