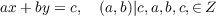The Diophantine equation ax + by = c in Q() and other number fields

David Rosen

Vol. 119 (1985), No. 2, 465–472

DOI: 10.2140/pjm.1985.119.465

Abstract

Solving in rational integers the linear diophantine equation

(1)

is very well known. Let d = (a,b), and put A = a∕d, B = b∕d, C = c∕d, then Equation (1) becomes

The purpose of this note is to discuss the solutions of this equation when A, B, C are integers in Q() and the solutions are integers in Q(). What makes the discussion interesting is that an algorithm which mimics the continued fraction algorithm that solves the rational integer case can be implemented.

Mathematical Subject Classification 2000

Primary: 11D04

Secondary: 11A55

Milestones

Received: 4 August 1983

Revised: 16 July 1984

Published: 1 October 1985