|
|||||

|

|
|

|

|
|
Pairs of positive
solutions of quasilinear elliptic equations in exterior
domains
Takaŝi Kusano, Charles Andrew Swanson and Hiroyuki Usami |
|
Vol. 120 (1985), No. 2, 385–399
|
Abstract |
|
Our main objective is to prove the existence of infinitely many pairs (u1,u2) of positive solutions of quasilinear elliptic differential equations 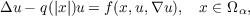 throughout exterior domains Ωα ⊂ RN, N ≥ 2, of the type 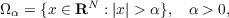 where x = (x1,…,xN), ∇u = (∂u∕∂x1,…,∂u∕∂xN), and Δ = ∇⋅∇. Each pair has the property that u1(x)∕u2(x) has uniform limit zero in Ωα as |x|→∞. In particular, if q(t) ≡ 0 and N ≥ 3, u1(x) has limit 0 as |x|→∞, and u2(x) is bounded above and below by positive constants in Ωα. |
Mathematical Subject Classification 2000
Primary: 35J65
|
Milestones
Received: 24 February 1984
Published: 1 December 1985
|
Authors |
| Takaŝi Kusano | |
| Charles Andrew Swanson | |
| Hiroyuki Usami | |
 |
