|
Let St(α) denote the
subclass of functions f(z) analytic in the open unit disk D which satisfy the
conditions f(0) = 0, f′(0) = 1 and Re(zf′(z)∕f(z))>α for z in D. In this note
we investigate the compact, convex family coS(St(α)) which is the closed
convex hull of the set of all functions analytic in D that are subordinate to
some function in St(α), α < 1∕2. The principal result establishes that every
support point of coS(St(α)) arising from a “nontrivial” functional must also be
an extreme point, hence a function of the form f(z) = xz∕(1 − yz)2(1−α),
|x| = |y| = 1.
To amplify on this synopsis, let 𝒜 denote the set of functions analytic in
the open unit disk D = {z ∈ C∣|z| < 1}. Then 𝒜 is a locally convex linear
topological space under the topology of uniform convergence on compact
subsets of D. A function f in 𝒜 is said to be subordinate to a function F in 𝒜
(written f ≺ F), if there is a function φ in B0 such that f(z) = F(φ(z)), where
B0 = {φ ∈𝒜|φ(0) = 0,|φ(z)| < 1 in D}.
Let ℱ be a compact subset of 𝒜. A function f in ℱ is a support point of ℱ if
there is a continuous linear functional J on 𝒜 such that
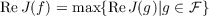
and ReJ is non-constant on ℱ. We use Σℱ to denote the set of support points of ℱ
and coℱ and ℰcoℱ to denote, respectively, the closed convex hull of ℱ and the set of
extreme points of the closed convex hull of ℱ.
|