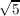The spacing of the minima in certain cubic lattices

Hugh C. Williams

Vol. 124 (1986), No. 2, 483–496

DOI: 10.2140/pjm.1986.124.483

Abstract

Let 𝒦 be a cubic field with negative discriminant; let μ,ν ∈𝒦; and let ℛ be a lattice with basis {1,μ,ν} such that 1 is a minimum of ℛ. If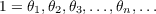

is a chain of adjacent minima of ℛ with 𝜃_i+1 > 𝜃_i (i = 1,2,3,…), then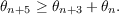

This result can be used to prove that if p is the period of Voronoi’s continued fraction algorithm for finding the fundamental unit 𝜖₀ of 𝒦, then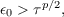

where τ = (1 + )∕2. It is also shown that

Mathematical Subject Classification 2000

Primary: 11R27

Secondary: 11R16, 11T06, 11Y40

Milestones

Received: 6 July 1984

Published: 1 October 1986