Range of Gateaux differentiable operators and local expansions

Jong Sook Bae and Sangsuk Yie

Vol. 125 (1986), No. 2, 289–300

DOI: 10.2140/pjm.1986.125.289

Abstract

Let X and Y be Banach spaces, and P : X → Y a Gateaux differentiable operator having closed graph. Suppose that there is a continuous function c : [0,∞) → (0,∞) satisfying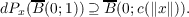

Then it is shown that for any K > 0 (possibly K = ∞), P(B(0;K)) contains B(P(0);∫ ₀^Kc(s)ds). Similar results are obtained for local expansions and locally strongly ϕ-accretive operators. These results extend a number of known theorems by giving the precise geometric estimations for normal solvability of Px = y.

Mathematical Subject Classification 2000

Primary: 47H06

Milestones

Received: 22 June 1985

Published: 1 December 1986