|

|

|
|
Analytic continuation
of local representations of Lie groups
Palle E. T. Jorgensen |
|
Vol. 125 (1986), No. 2, 397–408
|
Abstract |
|
We consider a symmetric space (G,K,σ) where G is a Lie group, K a closed subgroup, and σ the involutive automorphism defining the space. A local representation π is defined for g in a neighborhood of e in G, and the operator π(g) is unbounded and defined on a dense subspace in a Hilbert space where the identity 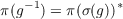 holds. We study analytic continuations of π to unitary representations of a group G∗ which is dual to G. |
Mathematical Subject Classification 2000
Primary: 22E45
|
Milestones
Received: 3 July 1985
Published: 1 December 1986
|
Authors |
| Palle E. T. Jorgensen | |
 |
