|
Let f(x) be a real analytic
function defined on a (possibly infinite and possibly closed) interval (A,B). The
frequency distribution of f is defined to be
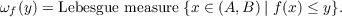
In this paper we consider the problem of determining f given its distribution ωf.
Since a trivial change of f of the form g(x) = f(a ± x) will have the same
distribution, we ask: does ωf determine f up to such trivial changes? A partial
answer is given by
Theorem. If f is real analytic with distinct and non-degenerate critical valves on a
finite interval [A,B] and if the values of f at the endpoints are different from
each other, and at least one is different from the value at any critical point
on the interior of the interval, then f is determined uniquely (up to trivial
changes) by its frequency distribution on this interval As a consequence we
have:
Corollary. A real analytic function with distinct non-degenerate critical values is
determined uniquely (up to trivial changes) by its frequency distribution on the interval
between its minimum and maximum critical points.
|