A generalization of a theorem of Delaunay to rotational W-hypersurfaces of σ_l-type in Hⁿ⁺¹ and Sⁿ⁺¹

Ivan Charles Sterling

Vol. 127 (1987), No. 1, 187–197

DOI: 10.2140/pjm.1987.127.187

Abstract

In 1841 Delaunay proved that if one rolls a conic section on a line in a plane and then rotates about that line the trace of a focus, one obtains a constant mean curvature surface of revolution in R³. Conversely, all such surfaces, except spheres, are constructed in this way. In 1981, Hsiang and Yu generalized Delaunay’s theorem to constant mean curvature rotation hypersurfaces in Rⁿ⁺¹. In 1982, Hsiang further generalized Delaunay’s theorem to rotational W-hypersurfaces of σ_l-type in Rⁿ⁺¹. These are hypersurfaces such that the l-th-basic symmetric polynomial of the principal curvatures (k_i(x)), namely,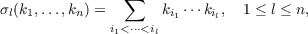

is constant.

Here we generalize Delaunay’s theorem to rotational W-hypersurfaces of σ_l-type in hyperbolic (n + 1)-space Hⁿ⁺¹ and spherical (n + 1)-space Sⁿ⁺¹. Specifically we generalize the “rolling construction” of Delaunay. Various geometrical properties of these surfaces and their generating curves have been studied by Hsiang.

Mathematical Subject Classification 2000

Primary: 53A10

Secondary: 53C42

Milestones

Received: 26 April 1985

Revised: 13 January 1986

Published: 1 March 1987