Eigenvalue estimates with applications to minimal surfaces

Johan Tysk

Vol. 128 (1987), No. 2, 361–366

DOI: 10.2140/pjm.1987.128.361

Abstract

We study eigenvalue estimates of branched Riemannian coverings of compact manifolds. We prove that if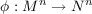

is a branched Riemannian covering, and {μ_i}_i=0^∞ and {λ_i}_i=0^∞ are the eigenvalues of the Laplace-Beltrami operator on M and N, respectively, then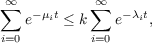

for all positive t, where k is the number of sheets of the covering. As one application of this estimate we show that the index of a minimal oriented surface in R³ is bounded by a constant multiple of the total curvature. Another consequence of our estimate is that the index of a closed oriented minimal surface in a flat three-dimensional torus is bounded by a constant multiple of the degree of the Gauss map.

Mathematical Subject Classification 2000

Primary: 53C42

Secondary: 35P15, 58G11, 58G25

Milestones

Received: 14 July 1986

Published: 1 June 1987