|
|||||

|

|
|

|

|
|
Topological
identification of multiple solutions to parametrized
nonlinear equations
Robert F. Brown |
|
Vol. 131 (1988), No. 1, 51–69
|
Abstract |
|
Let L : E → F be an isomorphism of Banach spaces, let H : E × Rn → F be a completely continuous mapping, and let B : E → Rn be a bounded linear mapping onto a euclidean space. The solutions (y,λ) to the problem 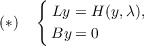 can be represented as the fixed points of a mapping T : E × Rn → E × Rn. Neilsen fixed point theory may be extended to produce lower bounds for the number of fixed points of such maps. Problems of the type (*) include boundary value problems for ordinary differential systems of the form: 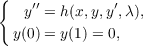 where y = y(x) : [0,1] → Rn and λ ∈ Rn, satisfying an additional condition such as y(1∕2) = 0 or ∫ 01y(t)dt = A for a given A ∈ Rn. |
Mathematical Subject Classification 2000
Primary: 47H15
Secondary: 34B15, 34G20, 47H10, 55M20
|
Milestones
Received: 20 February 1986
Published: 1 January 1988
|
Authors |
| Robert F. Brown | |
| Department of Mathematics University of California,Los Angeles Los Angeles CA 90095-1555 United States |
|
| http://www.math.ucla.edu/~rfb/ | |
 |
