Weighted norm inequalities for the Fourier transform on connected locally compact groups

Jeffrey A. Hogan

Vol. 131 (1988), No. 2, 277–290

DOI: 10.2140/pjm.1988.131.277

Abstract

Let G be a locally compact connected group. If G is also either compact or abelian, sufficient conditions on a non-negative pair of measurable functions T and V are given to imply that there exists a constant c independent of f for which an inequality of the form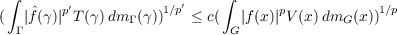

holds for all integrable f on G (1 < p ≤ 2,p′ = p∕(p − 1)). Here, f denotes the Fourier transform of f defined on Γ (the dual of G) and m_G, m_Γ are Haar measures on G, Γ respectively. Conditions on T, V are also given to esnure that the inequality holds with p′ replaced by a more general exponent on a more restricted class of groups.

Mathematical Subject Classification 2000

Primary: 43A25

Secondary: 43A15, 43A30

Milestones

Received: 21 September 1986

Published: 1 February 1988