Invariant subspaces of ℋ² of an annulus

Daniel Hitt

Vol. 134 (1988), No. 1, 101–120

DOI: 10.2140/pjm.1988.134.101

Abstract

Fully invariant subspaces of the Hardy class ℋ²(G) on a multiply connected domain G ⊂ C, are those ℳ such that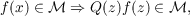

for all rational functions Q whose poles are in the complement of G. Simply invariant subspaces are those ℳ such that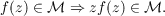

Although the structure of the fully invariant subspaces is well known as a result of the work of Sarason, Hasumi, and Voichick, little work has been done on subspaces simply invariant but not fully invariant. In this paper we consider the special case G = A, where A denotes the annulus {z ∈ C : 1 < |z| < R}. We classify the simply invariant (closed) subspaces ℳ of ℋ²(A).

Mathematical Subject Classification 2000

Primary: 46E20

Secondary: 46J15, 47A15, 47B38

Milestones

Received: 10 June 1986

Published: 1 September 1988