Integral logarithmic means for regular functions

C. N. Linden

Vol. 138 (1989), No. 1, 119–127

DOI: 10.2140/pjm.1989.138.119

Abstract

For a function f, regular in the unit disc, integral logarithmic means are defined by the formulae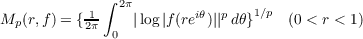

for 0 < p < ∞. These are related to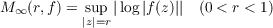

when the latter increases sufficiently rapidly. Thus when λ_∞(f) ≥ 1 the orders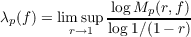

are continuous at infinity in the sense that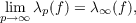

a property which does not generally hold when λ_∞(f) < 1. It transpires that in the extreme cases λ_∞(f) = λ₁(f) + 1, and λ_∞(f) = λ₁(f) ≥ 1, λ_p(f) is uniquely determined for 1 < p < ∞.

Mathematical Subject Classification 2000

Primary: 30D60

Secondary: 30C45

Milestones

Received: 23 November 1987

Published: 1 May 1989