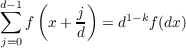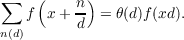|
Carlitz and others have proved
that if f is a polynomial such that it satisfies the formula
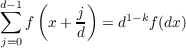 | (1.1) |
then f is (essentially) the k-th degree Bernoullli polynomial. The purpose of this
paper is to discuss the slightly more general formula
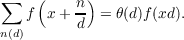 | (1.2) |
when f is periodic with period 1. The notation n(d) under the summation sign
indicates that n runs through a complete system of residues mod d. Formulae like
(1.1) and (1.2) occur also in theories of Franel’s formula and in the elementary theory
of Dedekind sums.
In this paper we will pretty much characterize the periodic bounded variation
solutions of (1.2). Then we provide a weak generalization of the current best form of
Franel’s theorem, and use this result to provide a method for constructing new
solutions of (1.2) from old ones, at least in principle.
|