|
For each odd prime power
q = pr we will investigate q − 2 different Cayley graphs called finite, upper half planes
over Fq. We define a finite, upper half-plane by
where Fq is the finite field with q elements and d is not a square in Fq. We define a
distance k between points z and w ∈ Hq by
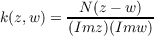 |
where Nz = zz and z = x − y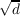 and Re z = x and Imz = y. We define a graph,
Xq(d,a), by letting the elements of Hq be the vertices of the graph and defining an
edge between z and w where k(z,w) = a for a fixed a ∈ Fq −{0}. We consider the
origin to be the point and Re z = x and Imz = y. We define a graph,
Xq(d,a), by letting the elements of Hq be the vertices of the graph and defining an
edge between z and w where k(z,w) = a for a fixed a ∈ Fq −{0}. We consider the
origin to be the point 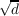 . We call Hq(d,a), the finite upper half-plane depending on
a fixed a and d. We first concern ourselves with whether the eigenvalues,
λ, of the adjacency matrices of the graphs satisfy the Ramanujan bound
|λ|≤ . We call Hq(d,a), the finite upper half-plane depending on
a fixed a and d. We first concern ourselves with whether the eigenvalues,
λ, of the adjacency matrices of the graphs satisfy the Ramanujan bound
|λ|≤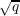 . Since the graphs are of degree q + 1, the paper shows a method to
use the representations for the additive and multiplicative groups of each
Fq to find the smaller associated isospectral matrices. We then find the
eigenvalues of the isospectral matrices. A computer program has verified
the Ramanujan bound for most of the graphs up to the prime power 35.
We next concern ourselves with the girth of the graphs. This paper shows
that the girths are either 3 or 4 and shows that the girth is 3 if a = 2d and
q ≡ 3(mod4) or if a and a − 3d are squares in Fq. The girth is 4 if a = 2d and
q ≡ 1(mod4). . Since the graphs are of degree q + 1, the paper shows a method to
use the representations for the additive and multiplicative groups of each
Fq to find the smaller associated isospectral matrices. We then find the
eigenvalues of the isospectral matrices. A computer program has verified
the Ramanujan bound for most of the graphs up to the prime power 35.
We next concern ourselves with the girth of the graphs. This paper shows
that the girths are either 3 or 4 and shows that the girth is 3 if a = 2d and
q ≡ 3(mod4) or if a and a − 3d are squares in Fq. The girth is 4 if a = 2d and
q ≡ 1(mod4).
|






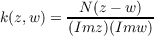
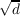 and Re
and Re 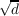 . We call
. We call 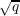 . Since the graphs are of degree
. Since the graphs are of degree 