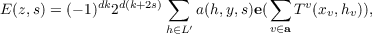|
This paper defines a
nonholomorphic Eisenstein series for a totally real algebraic number field F and the
special orthogonal group with respect to a bilinear form S = 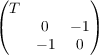 , where
T ∈ Mn(F) and its embedded images Tv ∈ Mn(ℝ) under archimedean places v of
F have signature (1,n − 1). This group has an associated product of tube
domains ℋa = Πv∈aℋv, the product taken over archimedean places of F and
each ℋv ⊂ ℂn. The series is denoted E(z,s;k,ψ,b) or simply E(z,s), with
z ∈ℋa, s ∈ ℂ a complex parameter, k ∈ ℤ the weight, ψ a Hecke character on
the ideles of F, and the level b an integral ideal in F. E has the Fourier
expansion , where
T ∈ Mn(F) and its embedded images Tv ∈ Mn(ℝ) under archimedean places v of
F have signature (1,n − 1). This group has an associated product of tube
domains ℋa = Πv∈aℋv, the product taken over archimedean places of F and
each ℋv ⊂ ℂn. The series is denoted E(z,s;k,ψ,b) or simply E(z,s), with
z ∈ℋa, s ∈ ℂ a complex parameter, k ∈ ℤ the weight, ψ a Hecke character on
the ideles of F, and the level b an integral ideal in F. E has the Fourier
expansion
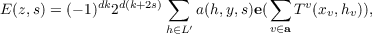 |
where d = [F : ℚ], L′ is the lattice dual to oFn under T, e(x) = e2πix, and
z = (xv + iyv)v∈a ∈ℋa. The Fourier coefficient a(h,y,s) is the product
(Nd)−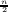 aa(h,y,s)af(h,s) with Nd the norm of the different of F over ℚ. The
archimedean factor is aa(h,y,s) = Πv∈aξ(yv,hv;k + s,s;Tv) with ξ a certain
confluent hypergeometric function studied by Shimura. The nonarchimedean factor
af(h,s) is essentially a product and quotient of Hecke L-functions, depending on the
parity of n and the nature of h. Specializing to s = 0 gives holomorphic and in special
cases nearly holomorphic behavior. aa(h,y,s)af(h,s) with Nd the norm of the different of F over ℚ. The
archimedean factor is aa(h,y,s) = Πv∈aξ(yv,hv;k + s,s;Tv) with ξ a certain
confluent hypergeometric function studied by Shimura. The nonarchimedean factor
af(h,s) is essentially a product and quotient of Hecke L-functions, depending on the
parity of n and the nature of h. Specializing to s = 0 gives holomorphic and in special
cases nearly holomorphic behavior.
|





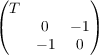 , where
, where