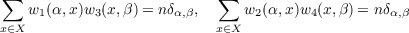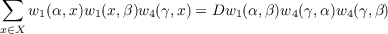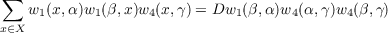|
The concept of spin model was
introduced by V. F. R. Jones. Kawagoe, Munemasa and Watatani generalized it by
dropping the symmetric condition, and defined a generalized spin model.
In this paper, by further generalizing the concept using four functions, we
define a generalized generalized spin model (four-weight spin model). Namely,
(X,w1,w2,w3,w4) is a generalized generalized spin model (four-weight spin model),
if X is a finite set and wi (i = 1,2,3,4) are complex valued functions on X × X
satisfying the following conditions:
 | (1) |
for any α, β in X,
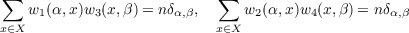 | (2) |
for any α and β in X,
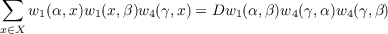 | (3a) |
and
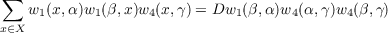 | (3b) |
for any α, β, and γ in X, where D2 = n = |X|.
We call as generalized spin models (two-weight spin models), the special cases of
generalized generalized spin models (four-weight spin models), where there are only
two functions w+ and w− from X × X to C with two of w1, w2, w3, w4 being in
{w+,tw+} and the remaining two of w1, w2, w3, w4 being in {w−,tw−}. We see that
we have three types of generalized spin models (two-weight spin models),
namely Jones type, pseudo-Jones type, and Hadamard type. We also see that
Kawagoe-Munemasa-Watatani’s generalized spin model is one special case of
Jones type, and Jones’ original spin model is a further special case of it.
Here we emphasize that there are actually interesting spin models which are
considerably different from the original concept of spin model defined by
Jones.
|