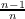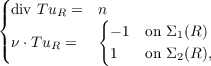|
|||||

|

|
|

|

|
|
Moon hypersurfaces
and some related existence results of capillary hypersurfaces
without gravity and of rotational symmetry
Fei-Tsen Liang |
|
Vol. 172 (1996), No. 2, 433–460
|
Mathematical Subject Classification 2000
Primary: 58E12
Secondary: 35J60, 53A10
|
Milestones
Received: 20 August 1993
Revised: 7 December 1993
Published: 1 February 1996
|
Authors |
| Fei-Tsen Liang | |
 |
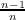 and
and