|
In this paper, we study several
properties of chaos of maps of compacta. We show that if a homeomorphism
f : X → X of a compactum X with dimX > 0 is continuum-wise expansive, then
there is an f-invariant closed subset Y of X with dimY > 0 such that f is (two-sided
strongly) chaotic on Y in the sense of Ruelle-Takens. Also, we investigate dynamical
properties of maps of graphs which are sensitive. In particular, we prove the
decomposition theorem of sensitive maps of graphs as follows: If f : G → G
is map of a graph G which is sensitive, then there exist finite subgraphs
Gi (1 ≤ i ≤ N) of G such that (a) each Gi is f-invariant and Gi ∩ Gj is
empty or a finite set for i≠j, (b) for each 1 ≤ i ≤ N, f is (two-sided strongly)
chaotic on Gi in the sense of Devaney and there exists a connected subgraph
Hi of Gi and a natural number n(i) ≥ 1 such that Hi is fn(i)-invariant,
fn(i)|fk(Hi) : fk(Hi) → fk(Hi) (0 ≤ k ≤ n(i) − 1) is topologically mixing,
∪k=0n(i)−1fk(Hi) = Gi, and fk(Hi) ∩ fk′(Hi) is empty or a finite set for
0 ≤ k < k′≤ n(i) − 1, and (c) dimF(f) ≤ 0, where
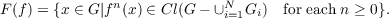
As a corollary, we show that in case of maps of graphs, chaos in the sense
of Ruelle-Takens is equal to (two-sided strongly) chaos in the sense of
Devaney, and sensitive maps of graphs induce two-sided chaos in the sense of
Li-Yorke.
|