Rational Pontryagin classes, local representations, and K^G-theory

Claude Schochet

Vol. 175 (1996), No. 1, 187–233

DOI: 10.2140/pjm.1996.175.187

Abstract

Suppose that X and Y are connected, simply connected Spin^c-manifolds of the same dimension. Let G be a compact connected Lie group with torsion-free fundamental group which acts upon X and Y such that X^G and Y ^G are non-empty and consist entirely of isolated fixed points. Suppose that f : X → Y is a smooth G-map such that the induced map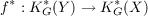

is an isomorphism. If X and Y are even-dimensional then for each fixed point x ∈ X^G, the local representations of G at x and at f(x) are equivalent. If f : X → Y is an equivalence then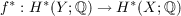

preserves Pontryagin classes.

Mathematical Subject Classification 2000

Primary: 57R20

Milestones

Received: 6 September 1993

Published: 1 September 1996