|
|||||

|

|
|

|

|
|
Lp-bounds for hypersingular integral
operators along curves
Sharad Chandarana |
|
Vol. 175 (1996), No. 2, 389–416
|
Abstract |
|
|
It is known that the Hilbert transform along curves: 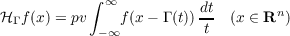 is bounded on LP, 1 < p < ∞, where Γ(t) is an appropriate curve in Rn. In particular, ∥ℋΓf∥p ≤ C∥f∥p, 1 < p < ∞, where Γ(t) = (t,|t|k sgnt),k ≥ 2, is a curve in R2. It is easy to see that the hypersingular integral operator 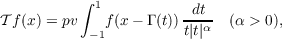 in which the singularity at the origin is worse than that in the Hilbert transform, is not bounded on L2(R2). To counterbalance this worsened singularity, we introduce an additional oscillation e−2πi|t|−β and study the operator 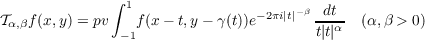 along the curve Γ(t) = (t,γ(t)), where γ(t) = |t|k or γ(t) = |t|k sgnt, k ≥ 2, in R2 and show that
|
Mathematical Subject Classification 2000
Primary: 42B25
Secondary: 44A15, 47B38
|
Milestones
Received: 15 July 1994
Revised: 7 December 1995
Published: 1 October 1996
|
Authors |
| Sharad Chandarana | |
| Department of Mathematics University of Wisconsin–Madison B127 Van Vleck Madison WI 53706 United States |
|
| http://www.math.wisc.edu/~chandara/ | |
 |

