|
Let 𝒳 be an open orientable
surface with finite genus and finite number of boundary components, and let 𝒴 be a
closed orientable surface. An open continuous function from 𝒳 to 𝒴 is termed a
(p,q)-map, 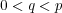 , if it has a finite number of branch points and assumes every
point in 𝒴 either p or q times, counting multiplicity, with possibly a finite number of
exceptions. These comprise the most general class of all nontrivial functions having
two valences between 𝒳 and 𝒴. , if it has a finite number of branch points and assumes every
point in 𝒴 either p or q times, counting multiplicity, with possibly a finite number of
exceptions. These comprise the most general class of all nontrivial functions having
two valences between 𝒳 and 𝒴.
In this paper we generalize and prove in a unified manner almost all the earlier
covering and existence results involving (p,q)-maps between orientable surfaces. Our
main tools are (i) a generalized embedding theorem (see Lyzzaik, 1995) which asserts
that image surfaces of (p,q)-maps embed in p-fold closed coverings possibly having
branch points off the image surfaces, and (ii) results (see Lyzzaik and Stephenson,
and Lyzzaik, 1996) “modifying” general (p,q)-maps to “simplicial” ones having the
same covering structures. This leads us to combinatorial results of (p,q)-maps
relating their branch orders and exceptional sets of points to the valences p,
q and the topological invariants of 𝒳 and 𝒴. The paper ends with open
questions.
|





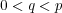 , if it has a finite number of branch points and assumes every
point in
, if it has a finite number of branch points and assumes every
point in 