On the average growth of Fourier coefficients of Siegel cusp forms of genus 2

Winfried Kohnen

Vol. 179 (1997), No. 1, 119–121

DOI: 10.2140/pjm.1997.179.119

Abstract

Let F be a Siegel cusp form of integral weight k on the Siegel modular group Sp₂(ℤ) of genus 2 and denote by a(T) (T ∈ Q^(2,2), T > 0 half-integral) its Fourier coefficients. It is known (see Böcherer & Raghavan, 1988 and Fomenko, 1987) that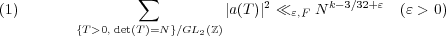

where the sum is over GL₂(ℤ)-classes of T > 0 with det(T) = N.

In the present note we shall give a result on the average growth of |a(T)|², where the average is taken w.r.t. the trace.

Milestones

Received: 17 June 1995

Published: 1 May 1997