|
|||||

|

|
|

|

|
|
Distortion theorems
for Bloch functions
Mario Bonk, David Minda and Hiroshi Yanagihara |
|
Vol. 179 (1997), No. 2, 241–262
|
Abstract |
|
A function f holomorphic on the unit disk 𝔻 is called a Bloch function if 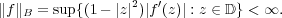 For α ∈ [0,1] let B1(α) denote the class of Bloch functions which have the normalization ∥f∥B ≤ 1, f(0) = 0 and f′(0) = α. A type of subordination theorem is established for B1(α). This theorem yields numerous sharp growth, distortion, curvature and covering theorems for B1(α). |
Milestones
Received: 1 September 1995
Published: 1 June 1997
|
Authors |
| Mario Bonk | |
| Tech. Univ. Braunschweig D-38106 Braunschweig Germany |
|
| David Minda | |
| University of Cincinnati Cincinnati, OH 45221-0025 |
|
| Hiroshi Yanagihara | |
| Yamaguchi University Tokiwadai, Ube Japan |
|
 |
