|
We derive estimates on
solutions u(k,x) to a scattering problem with variable index of refraction in three
space dimensions. To be precise, suppose n(x) ∈ C∞(ℝ3) is positive and n(x) = 1 for
|x|≥ R. We want to estimate solutions u(k,x) to
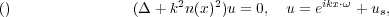
where us satisfies the radiation condition. Here, k ∈ ℝ denotes the frequency. There
are two mechanisms that can make u(k,x) large. One is the presence of
trapped rays. In this work we assume there are no trapped rays. The other
mechanism is the focusing of waves, i.e., the formation of caustics. Our primary
goal here is to estimate the effect of this mechanism, without making any
hypothesis on the geometrical nature of whatever caustics might arise. We show
that

where ⟨k⟩ = (1 + k2)1∕2.
|