|
Suppose C is an algebraic
curve, f is a rational function on C defined over ℚ, and 𝒜 is a fractional ideal of ℚ. If
f is not equivalent to a polynomial, then Siegel’s theorem gives a necessary
condition for the set C(ℚ) ∩ f−1(𝒜) to be infinite: C is of genus 0 and the
fiber f−1(∞) consists of two conjugate quadratic real points. We consider a
converse. Let 𝒫 be a parameter space for a smooth family Φ : 𝒯 →𝒫× ℙ1
of (degree n) genus 0 curves over ℚ. That is, the fiber 𝒯 of points of 𝒯
over of points of 𝒯
over 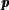 × ℙ1 has genus 0 for × ℙ1 has genus 0 for 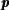 ∈𝒫. Assume a Zariski dense set of ∈𝒫. Assume a Zariski dense set of 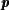 ∈𝒫(ℚ)
have fiber Φ ∈𝒫(ℚ)
have fiber Φ −1( −1(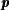 ×∞) over ∞ consisting of two conjugate quadratic real
points. The family Φ is then a Siegel family. We ask when the conclusion of
Siegel’s theorem — Φ ×∞) over ∞ consisting of two conjugate quadratic real
points. The family Φ is then a Siegel family. We ask when the conclusion of
Siegel’s theorem — Φ (ℚ) ∩𝒜 is infinite — holds for a Zariski dense subset of (ℚ) ∩𝒜 is infinite — holds for a Zariski dense subset of
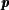 ∈𝒫(ℚ). ∈𝒫(ℚ).
We show how braid action on covers and Hurwitz spaces can tackle this. It refines
a unirationality criterion for Hurwitz spaces. A particular family, 10Φ′, of degree 10
rational functions, illustrates this. It arises as the exceptional case for a general result
on Hilbert’s Irreducibility Theorem. Fried, 1986 says the only indecomposable
polynomials f(y) ∈ ℚ[y] with f(y) − t reducible in ℚ[y] for infinitely many
t ∈𝒜∖ f(ℚ) have degree 5. We show the family 10Φ′ satisfies the converse to
Siegel’s theorem. Thus, exceptional polynomials of degree 5 in Fried, 1986 do
exist.
We suspect this result generalizes, thus codifying arithmetic accidents occurring
in 10𝒫′. To illustrate, we’ve cast this paper as a collection of elementary group theory
tools for extracting from a family of covers special cases with specific arithmetic
properties. Examples of Siegel and Néron families show the efficiency of the tools,
though each case leaves a diophantine mystery.
|





 of points of
of points of