|
|||||

|

|
|

|

|
|
Topology versus Chern
numbers for complex 3-folds
Claude LeBrun |
|
Vol. 191 (1999), No. 1, 123–131
|
Abstract |
|
We show by example that the
Chern numbers |
Milestones
Received: 19 February 1998
Published: 1 November 1999
|
Authors |
| Claude LeBrun | |
| SUNY Stony Brook Stony Brook, NY 11794 |
|
 |
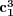 and
and 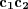 of a complex
of a complex 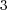 -fold are not determined by the
topology of the underlying smooth compact
-fold are not determined by the
topology of the underlying smooth compact 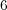 -manifold. In fact, we observe that
infinitely many different values of a Chern number can be achieved by (integrable)
complex structures on a fixed
-manifold. In fact, we observe that
infinitely many different values of a Chern number can be achieved by (integrable)
complex structures on a fixed 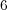 -manifold.
-manifold.