|
|||||

|

|
|

|

|
|
How large are the
spectral gaps?
Alex Iosevich and Steen Pedersen |
|
Vol. 192 (2000), No. 2, 307–314
|
Abstract |
|
Let D be a bounded domain in ℝn whose boundary has a Minkowski dimension α < n. Suppose that EΛ={e2πix⋅λ}λ∈Λ, Λ an infinite discrete subset of ℝn, is a frame of exponentials for L2(D), with frame constants A,B, A ≤ B. Then if 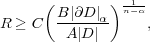 where C depends only on the ambient dimension n and |∂D|α denotes the Minkowski content, then every cube of sidelength R contains at least one element of Λ. We give examples that illustrate the extent to which our estimates are sharp. |
Milestones
Received: 25 June 1998
Published: 1 February 2000
|
Authors |
| Alex Iosevich | |
| Wright State University Dayton OH 45435 |
|
| Steen Pedersen | |
| Wright State University Dayton OH 45435 |
Department of Mathematics Georgetown University Washington, DC 20057 |
 |
