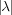|
|||||

|

|
|

|

|
|
L2
spectral decomposition on the Heisenberg group associated to
the action of U(p,q)
T. Godoy and L. Saal |
|
Vol. 193 (2000), No. 2, 327–353
|
Abstract |
|
Here we consider the
Heisenberg group Hn = Cn ×ℜ. U Let 
Via the Plancherel inversion formula, we obtain the joint spectral decomposition
of L2  where each Sλ.k is a tempered distribution U |
Milestones
Received: 11 August 1998
Published: 1 April 2000
|
Authors |
| T. Godoy | |
| Facultad de Matemática, Astronomía y
Física Universidad Nacional de Cordoba Ciudad Universitaria 5000 Cordoba Argentina |
|
| L. Saal | |
| Facultad de Matemática, Astronomía y
Física Universidad Nacional de Cordoba Ciudad Universitaria 5000 Cordoba Argentina |
|
 |



 be the standard basis of the Lie algebra of
be the standard basis of the Lie algebra of  with respect to
with respect to  invariant satisfying
invariant satisfying