|
For a compact Riemann surface X of genus g > 1,
Hom(π1(X),PU(p,q))∕PU(p,q) is the moduli space of flat PU(p,q)-connections
on X. There are two integer invariants, dP,dQ, associated with each
σ ∈ Hom(π1(X),PU(p,q))∕ PU(p,q). These invariants are related to the
Toledo invariant τ by τ = 2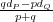 . This paper shows, via the theory of
Higgs bundles, that if q = 1, then −2(g − 1) ≤ τ ≤ 2(g − 1). Moreover,
Hom(π1(X),PU(2,1))∕PU(2,1) has one connected component corresponding to each
τ ∈ . This paper shows, via the theory of
Higgs bundles, that if q = 1, then −2(g − 1) ≤ τ ≤ 2(g − 1). Moreover,
Hom(π1(X),PU(2,1))∕PU(2,1) has one connected component corresponding to each
τ ∈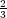 ℤ with −2(g − 1) ≤ τ ≤ 2(g − 1). Therefore the total number of connected
components is 6(g − 1) + 1. ℤ with −2(g − 1) ≤ τ ≤ 2(g − 1). Therefore the total number of connected
components is 6(g − 1) + 1.
|





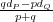 . This paper shows, via the theory of
Higgs bundles, that if
. This paper shows, via the theory of
Higgs bundles, that if