A note on generalized Bernoulli numbers

Kwang-Wu Chen and Minking Eie

Vol. 199 (2001), No. 1, 41–59

DOI: 10.2140/pjm.2001.199.41

Abstract

In this paper, we consider the zeta function Z(P,χ,s) associated with a polynomial P(X) ∈ ℝ[X₁,…,X_r] and χ = (χ₁,…,χ_r) with χ_j non-trivial Dirichlet characters, defined by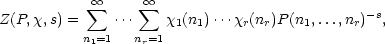

which is absolutely convergent for sufficiently large Re s under some conditions on P(X). We shall prove that the special value Z(P,χ,−m) is completely determined by P^m(X) in a simple way. As an immediate application, we give a closed expression for sums of products of any number of generalized Bernoulli numbers.

Milestones

Received: 9 July 1999

Revised: 30 December 1999

Published: 1 May 2001