|
|||||

|

|
|

|

|
|
Prescribing scalar
curvature on Sn
Wenxiong Chen and Congming Li |
|
Vol. 199 (2001), No. 1, 61–78
|
Abstract |
|
We consider the prescribing scalar curvature equation 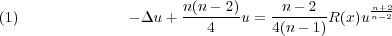 on Sn for n ≥ 3. In the case R is rotationally symmetric, the well-known Kazdan–Warner condition implies that a necessary condition for (1) to have a solution is: R > 0 somewhere and R′(r) changes signs. Then, (a) is this a sufficient condition? (b) If not, what are the necessary and sufficient conditions? These have been open problems for decades. In Chen & Li, 1995, we gave question (a) a negative answer. We showed that a necessary condition for (1) to have a solution is: 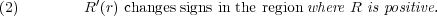 Now is this also a sufficient condition? In this paper, we prove that if R(r) satisfies the ‘flatness condition’, then (2) is the necessary and sufficient condition for (1) to have a solution. This essentially answers question (b). We also generalized this result to non-symmetric functions R. Here the additional ‘flatness condition’ is a standard assumption which has been used by many authors to guarantee the existence of a solution. In particular, for n = 3, ‘non-degenerate’ functions satisfy this condition. Based on Theorem 3 in Chen & Li, 1995, we also show that for some rotationally symmetric R, (1) is solvable while none of the solutions is rotationally symmetric. This is interesting in the studying of symmetry breaking. |
Milestones
Received: 15 September 1998
Published: 1 May 2001
|
Authors |
| Wenxiong Chen | |
| Department of Mathematics Southwest Missouri State University Springfield, MO 65807 |
|
| Congming Li | |
| Department of Applied
Mathematics University of Colorado at Boulder Boulder, CO 80039 |
|
 |
