|
|||||

|

|
|

|

|
|
The domain algebra of
a CP-semigroup
William Arveson |
|
Vol. 203 (2002), No. 1, 67–77
|
Abstract |
|
A CP-semigroup (or quantum dynamical semigroup) is a semigroup ϕ = {ϕt : t ≥ 0} of normal completely positive linear maps on ℬ(H), H being a separable Hilbert space, which satisfies ϕt(1) = 1 for all t ≥ 0 and is continuous in the time parameter t the natural sense. Let 𝒟 be the natural domain of the generator L of ϕ, ϕt = exptL, t ≥ 0. Since the maps ϕt need not be multiplicative 𝒟 is typically an operator space, but not an algebra. However, in this note we show that the set of operators 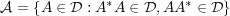 is a ∗-subalgebra of ℬ(H), indeed 𝒜 is the largest self-adjoint algebra contained in 𝒟. Examples are described for which the domain algebra 𝒜 is, and is not, strongly dense in ℬ(H). |
Milestones
Received: 30 May 2000
Revised: 7 March 2001
Published: 1 March 2002
|
Authors |
| William Arveson | |
| Department of Mathematics University of California, Berkeley Berkeley CA 94720 |
|
 |
