|
Let F be a global field with
char(F)≠2 and K an algebraic function field in one variable of genus zero over F. In
this paper, we investigate two kinds of Hasse principles for Brauer classes on K. If
Br(K) is the Brauer group of K and Br(K)′ is the subgroup of Br(K) whose
elements have order relatively prime to char(F), then we precisely determine the
kernels of the maps
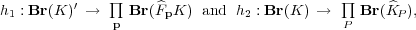
where p runs over the prime spots of F and P runs over the places of K which are
trivial over F, and Fp, KP are the completions at p, P respectively. To
facilitate the determination of these kernels, we compute the kernel of the map
h : Br(K) → ∏
P Br(KV P) where V P is the residue field with respect to P and
show that the kernels of these three maps coincide. We then consider a more
general version of the maps above by describing the 2-torsion subgroup of
the kernel of h1 when a finite number of prime spots in the product are
omitted.
|