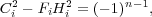|
Solving Pell’s equation is of
relevance in finding fundamental units in real quadratic fields and for this reason
polynomial solutions are of interest in that they can supply the fundamental units in
infinite families of such fields.
In this paper an algorithm is described which allows one to construct, for each
positive integer n, a finite collection, {Fi}, of multi-variable polynomials
(with integral coefficients), each satisfying a multi-variable polynomial Pell’s
equation
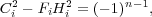
where Ci and Hi are multi-variable polynomials with integral coefficients. Each
positive integer whose square-root has a regular continued fraction expansion
with period n + 1 lies in the range of one of these polynomials. Moreover,
the continued fraction expansion of these polynomials is given explicitly as
is the fundamental solution to the above multi-variable polynomial Pell’s
equation.
Some implications for determining the fundamental unit in a wide class of real
quadratic fields is considered.
|