|
|||||

|

|
|

|

|
|
Partial regularity
for weak solutions of semilinear elliptic equations with
supercritical exponents
Zongming Guo and Jiayu Li |
|
Vol. 214 (2004), No. 1, 89–107
|
Abstract |
|
Let Ω be an open subset in Rn (n ≥ 3). In this paper, we study the partial regularity for stationary positive weak solutions of the equation 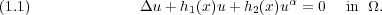 We prove that if α > |
Milestones
Received: 30 January 2001
Revised: 24 June 2002
Published: 1 March 2004
|
Authors |
| Zongming Guo | |
| Department of Mathematics Donghua University Shanghai 200051 P.R. China |
|
| Jiayu Li | |
| Institute of Mathematics Fudan University and Academia Sinica Beijing, 100080 P.R. China |
|
 |
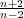 , and
, and 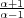 , which generalizes the main results in Pacard 1993 and Pacard
1994.
, which generalizes the main results in Pacard 1993 and Pacard
1994.