|
Let MHL and MS respectively
denote the Hardy–Littlewood and strong maximal operators, and let Mx and My
respectively denote the one-dimensional Hardy–Littlewood maximal operators
in the horizontal and vertical directions in R2. It is well known that if f
and f are equidistributed functions supported on Q = [0,1] × [0,1], then
∫
QMHLf ∼∫
QMHLf. This article examines the relationships between ∫
QMyf and
∫
QMyf, ∫
QMyMxf and ∫
QMyMxf, and ∫
QMSf and ∫
QMSf in the
scenario in which f and f are horizontal rearrangements of one another,
meaning that f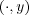 and f and f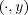 are equidistributed on are equidistributed on ![[0,1]](a072x.png) for any value of
y. for any value of
y.
The rearrangement results provided are not only of intrinsic interest, but also
yield tools for more detailed examinations involving the local integrablility of
maximal functions. They are used in a companion paper to prove that if f is
supported on Q, ∫
QMyMxf < ∞, and ∫
QMxMyf = ∞, then there exists a set A
of finite measure in R2 such that ∫
AMSf = ∞.
|





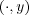 and
and 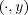 are equidistributed on
are equidistributed on ![[0,1]](a072x.png) for any value of
for any value of
