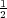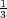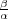|
|||||

|

|
|

|

|
|
Tight contact
structures of certain Seifert fibered 3-manifolds with
e0 = −1
Jinhong Kim |
|
Vol. 221 (2005), No. 1, 109–122
|
Abstract |
|
We classify, up to contact
isotopy, all tight contact structures on a family of Seifert fibered three-manifolds
M |
Keywords
tight contact structure, Seifert fibered 3-manifold,
truncated Euler number
|
Mathematical Subject Classification 2000
Primary: 57R57
|
Milestones
Received: 9 October 2003
Revised: 18 October 2004
Accepted: 5 December 2004
Published: 1 September 2005
|
Authors |
| Jinhong Kim | |
| Department of Mathematics KAIST, Kusong-dong, Yusong-gu Daejon 305–701 South Korea |
|
 |



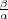

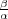
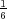 . We show that, if
. We show that, if 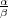 , there are exactly
, there are exactly