|
|||||

|

|
|

|

|
|
A generalization of
Gauchman’s rigidity theorem
Hong-Wei Xu, Wang Fang and Fei Xiang |
|
Vol. 228 (2006), No. 1, 185–199
|
Abstract |
|
We generalize the
well-known Gauchman theorem for closed minimal submanifolds in a unit sphere, and
prove that if M is an n-dimensional closed submanifold of parallel mean curvature in
Sn+p and if σ(u) ≤ |
Keywords
closed submanifolds, rigidity theorem, parallel mean
curvature
|
Mathematical Subject Classification 2000
Primary: 53C40, 53C42
|
Milestones
Received: 12 February 2005
Accepted: 6 July 2005
Published: 1 November 2006
|
Authors |
| Hong-Wei Xu | |
| Center of Mathematical
Sciences Zhejiang University Hangzhou 310027 The People’s Republic of China |
|
| Wang Fang | |
| Center of Mathematical
Sciences Zhejiang University Hangzhou 310027 The People’s Republic of China |
|
| Fei Xiang | |
| Center of Mathematical
Sciences Zhejiang University Hangzhou 310027 The People’s Republic of China |
|
 |
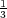 for any unit vector
for any unit vector 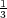 . Moreover, we give a geometrical
classification of closed submanifolds with parallel mean curvature satisfying
. Moreover, we give a geometrical
classification of closed submanifolds with parallel mean curvature satisfying
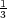 .
.