|
|||||

|

|
|

|

|
|
An absolute estimate
of the homogeneous expansions of holomorphic mappings
Taishun Liu and Jianfei Wang |
|
Vol. 231 (2007), No. 1, 155–166
|
Abstract |
|
Let f : Ω → Ω be a holomorphic mapping, where Ω is one of the four classical domains in ℂm×n. We show that, if P = f(0), we have ![∞∑ ∥DφP-(P)[Dkf-(0)(Zk-)]∥Ω-
k!∥DφP (P)∥ < 1
k=0](a090x.png) for ∥Z∥Ω < |
Keywords
holomorphic mapping, homogeneous expansion, classical
domains, Bohr’s theorem
|
Mathematical Subject Classification 2000
Primary: 30H05
Secondary: 32A05
|
Milestones
Received: 23 December 2005
Revised: 25 September 2006
Accepted: 26 October 2006
Published: 1 May 2007
|
Authors |
| Taishun Liu | |
| Department of Mathematics Huzhou Teachers College Huzhou, Zhejiang, 313000 China |
|
| Jianfei Wang | |
| Department of Mathematics University of Science and Technology of China Hefei, Anhui, 230026 China |
|
 |
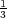 and
and  is the best possible.
is the best possible.