|
|||||

|

|
|

|

|
|
The braid group
surjects onto G2 tensor space
Scott Morrison |
|
Vol. 249 (2011), No. 1, 189–198
|
Abstract |
|
Let V be the 7-dimensional irreducible representation of the quantum group Uq(g2). For each n, there is a map from the braid group ℬn to the endomorphism algebra of the n-th tensor power of V , given by ℛ matrices. Extending linearly to the braid group algebra, we get a map 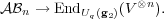 Lehrer and Zhang have proved that map is surjective, as a special case of a more general result. Using Kuperberg’s spider for G2, we give an elementary diagrammatic proof of this result. |
Keywords
braid group, spider, G2, tensor category, representation
theory
|
Mathematical Subject Classification 2000
Primary: 17B37
Secondary: 20G42, 17B10, 18D10
|
Supplementary material |
Milestones
Received: 22 September 2009
Revised: 4 January 2010
Accepted: 4 January 2010
Published: 3 January 2011
|
Authors |
| Scott Morrison | |
| Microsoft Station Q CNSI Building University of California Santa Barbara, CA 93106-6105 |
|
| http://tqft.net/ | |
 |
