|
|||||

|

|
|

|

|
|
Mixed interior and
boundary nodal bubbling solutions for a sinh-Poisson equation
Juncheng Wei, Long Wei and Feng Zhou |
|
Vol. 250 (2011), No. 1, 225–256
|
Abstract |
|
We consider here the semilinear equation Δu + 2𝜀2 sinhu = 0 posed on a bounded smooth domain Ω in ℝ2 with homogeneous Neumann boundary condition, where 𝜀 > 0 is a small parameter. We show that for any given nonnegative integers k and l with k + l ≥ 1, there exists a family of solutions u𝜀 that develops 2k interior and 2l boundary singularities for 𝜀 sufficiently small, with the property that 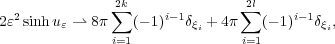 where (ξ1,…,ξ2(k+l)) are critical points of some functional defined explicitly in terms of the associated Green function. |
Keywords
boundary-interior nodal bubbling solutions, sinh-Poisson equation
|
Mathematical Subject Classification 2000
Primary: 35J20, 35J65
|
Milestones
Received: 3 January 2010
Accepted: 18 February 2010
Published: 1 March 2011
|
Authors |
| Juncheng Wei | |
| Department of Mathematics The Chinese University of Hong Kong Room 220, Lady Shaw Building Shatin, Hong Kong Hong Kong |
|
| Long Wei | |
| Institute of Applied Mathematics and
Engineering Computations Hangzhou Dianzi University Hangzhou, Zhejiang 310018 China |
|
| Feng Zhou | |
| Department of Mathematics East China Normal University Shanghai 200062 China |
|
 |
