|
|||||

|

|
|

|

|
|
Two
Kazdan–Warner-type identities for the renormalized volume
coefficients and the Gauss–Bonnet curvatures of a Riemannian
metric
Bin Guo, Zheng-Chao Han and Haizhong Li |
|
Vol. 251 (2011), No. 2, 257–268
|
Abstract |
|
We prove two Kazdan–Warner-type identities involving the renormalized volume coefficients v(2k) of a Riemannian manifold (Mn,g), the Gauss–Bonnet curvature G2r, and a conformal Killing vector field on (Mn,g). In the case when the Riemannian manifold is locally conformally flat, we find 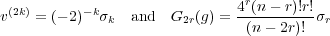 and our results reduce to earlier ones established by Viaclovsky in 2000 and the second author in 2006. |
Keywords
renormalized volume coefficients, v(2k) curvature, conformal transformation,
locally conformally flat, σk
curvature, Gauss–Bonnet curvatures, Kazdan–Warner
|
Mathematical Subject Classification 2000
Primary: 53C20
Secondary: 53A30
|
Milestones
Received: 18 May 2010
Accepted: 1 June 2010
Published: 3 June 2011
|
Authors |
| Bin Guo | |
| Department of Mathematical
Sciences Tsinghua University Beijing 100084 China |
Department of Mathematics Rutgers University 110 Frelinghuysen Road Piscataway, NJ 08854 United States |
| Zheng-Chao Han | |
| Department of Mathematics Rutgers University 110 Frelinghuysen Road Piscataway, NJ 08854 United States |
|
| Haizhong Li | |
| Department of Mathematical
Sciences Tsinghua University Beijing 100084 China |
|
 |
