|
|||||

|

|
|

|

|
|
Some Dirichlet
problems arising from conformal geometry
Qi-Rui Li and Weimin Sheng |
|
Vol. 251 (2011), No. 2, 337–359
|
Abstract |
|
We study the problem of finding complete conformal metrics determined by some symmetric function of the modified Schouten tensor on compact manifolds with boundary; which reduces to a Dirichlet problem. We prove the existence of the solution under some suitable conditions. In particular, we prove that every smooth compact n-dimensional manifold with boundary, with n ≥ 3, admits a complete Riemannian metric g whose Ricci curvature Ricg and scalar curvature Rg satisfy 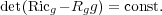 This result generalizes Aviles and McOwen’s in the scalar curvature case. |
Keywords
modified Schouten tensor, Dirichlet problem, complete
metric, prescribed curvature
|
Mathematical Subject Classification 2000
Primary: 53C21
Secondary: 53C23
|
Milestones
Received: 14 May 2010
Revised: 23 February 2011
Accepted: 15 March 2011
Published: 3 June 2011
|
Authors |
| Qi-Rui Li | |
| Department of Mathematics Zhejiang University Hangzhou 310027 China |
|
| Weimin Sheng | |
| Department of Mathematics Zhejiang University Hangzhou 310027 China |
|
 |
