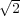|
|||||

|

|
|

|

|
|
Average Mahler’s
measure and Lp norms of unimodular polynomials
Kwok-Kwong Stephen Choi and Michael J. Mossinghoff |
|
Vol. 252 (2011), No. 1, 31–50
|
Abstract |
|
A polynomial f ∈ ℂ[z] is
unimodular if all its coefficients have unit modulus. Let Un denote the set of
unimodular polynomials of degree n− 1, and let Un∗ denote the subset of reciprocal
unimodular polynomials, which have the property that f(z) = ωzn−1f(1∕z) for some
complex number ω with |ω| = 1. We study the geometric and arithmetic mean values
of both the normalized Mahler’s measure M(f)∕ |
Keywords
mean Mahler’s measure, mean Lp
norm, unimodular polynomial, Littlewood polynomial
|
Mathematical Subject Classification 2010
Primary: 30C10, 11R06
Secondary: 11C08, 60G99
|
Milestones
Received: 14 June 2010
Accepted: 30 September 2010
Published: 8 October 2011
Proposed: Jonathan D. Rogawski
|
Authors |
| Kwok-Kwong Stephen Choi | |
| Department of Mathematics Simon Fraser University Burnaby, British Columbia V5A 1S6 Canada |
|
| http://www.math.sfu.ca/~kkchoi | |
| Michael J. Mossinghoff | |
| Department of Mathematics Davidson College Davidson, North Carolina 28035-6996 United States |
|
| http://www.davidson.edu/math/mossinghoff | |
 |
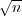 and
and 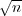 over the
sets
over the
sets