|
|||||

|

|
|

|

|
|
Axial symmetry and
regularity of solutions to an integral equation in a
half-space
Guozhen Lu and Jiuyi Zhu |
|
Vol. 253 (2011), No. 2, 455–473
|
Abstract |
|
We consider the integral equation 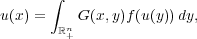 where G(x,y) is the Green’s function of the corresponding polyharmonic Dirichlet problem in a half-space. We prove by the method of moving planes in integral form that, under some integrability conditions, the solutions are axially symmetric with respect to some line parallel to the xn-axis and nondecreasing in the xn direction, which further implies the nonexistence of solutions. We also show similar results for a class of systems of integral equations. This appears to be the first paper in which the moving plane method in integral form is employed in a half-space to derive axial symmetry. We also obtain the regularity of the integral equation in a half-space 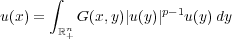 by the regularity lifting method. As a corollary, we prove the nonexistence of nonnegative solutions to this equation. Moreover, we show that the nonnegative solutions in this equation only depend on xn if u ∈ Lloc2n∕(n−2m)(ℝ+n) and 1 < p < (n + 2m)∕(n − 2m). |
Keywords
axial symmetry, regularity of solutions, half-space,
Green’s functions for polyharmonic operators, integral
equation, nonexistence of solutions
|
Mathematical Subject Classification 2010
Primary: 35J60
Secondary: 45G15
|
Milestones
Received: 9 September 2010
Revised: 30 May 2011
Accepted: 11 July 2011
Published: 21 January 2012
|
Authors |
| Guozhen Lu | |
| Department of Mathematics Wayne State University Detroit MI 48202 United States |
|
| http://www.math.wayne.edu/~gzlu | |
| Jiuyi Zhu | |
| Department of Mathematics Wayne State University Detroit MI 48202 United States |
|
 |
