Extension of an analytic disc and domains in ℂ² with noncompact automorphism group

Minju Song

Vol. 254 (2011), No. 1, 227–238

DOI: 10.2140/pjm.2011.254.227

Abstract

Let Ω be a smoothly bounded domain in ℂ² such that the Bergman representative map near the boundary continues to be diffeomorphic up to the boundary. If such a domain admits a holomorphic automorphism group orbit accumulating at a boundary point of finite D’Angelo type 2m, we show that the domain Ω is biholomorphic to the Thullen domain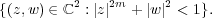

This result refines the well-known theorem of E. Bedford and S. Pinchuk.

Keywords

automorphism group action, Bergman representative map

Mathematical Subject Classification 2000

Primary: 32M05

Secondary: 32D15

Milestones

Received: 10 June 2010

Revised: 24 November 2010

Accepted: 27 November 2010

Published: 7 February 2012

Proposed: Kefeng Liu