|
|||||

|

|
|

|

|
|
Remarks on the
curvature behavior at the first singular time of the Ricci
flow
Nam Q. Le and Natasa Sesum |
|
Vol. 255 (2012), No. 1, 155–175
|
Abstract |
|
We study the curvature behavior at the first singular time of a solution to the Ricci flow 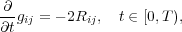 on a smooth, compact n-dimensional Riemannian manifold M. If the flow has uniformly bounded scalar curvature and develops Type I singularities at T, we show that suitable blow-ups of the evolving metrics converge in the pointed Cheeger–Gromov sense to a Gaussian shrinker by using Perelman’s 𝒲-functional. If the flow has uniformly bounded scalar curvature and develops Type II singularities at T, we show that suitable scalings of the potential functions in Perelman’s entropy functional converge to a positive constant on a complete, Ricci flat manifold. We also show that if the scalar curvature is uniformly bounded along the flow in certain integral sense then the flow either develops a Type II singularity at T or it can be smoothly extended past time T. |
Keywords
Ricci flow, scalar curvature, evolution
|
Mathematical Subject Classification 2010
Primary: 53C44
Secondary: 35K10
|
Milestones
Received: 7 October 2010
Revised: 23 February 2011
Accepted: 11 April 2011
Published: 14 March 2012
|
Authors |
| Nam Q. Le | |
| Department of Mathematics Columbia University New York NY 10027 United States |
|
| Natasa Sesum | |
| Department of Mathematics Rutgers University Piscataway NJ 10027 United States |
|
| http://www.math.rutgers.edu/~natasas | |
 |
