|
|||||

|

|
|

|

|
|
Deformation retracts
to the fat diagonal and applications to the existence of peak
solutions of nonlinear elliptic equations
E. Norman Dancer, Jonathan Hillman and Angela Pistoia |
|
Vol. 256 (2012), No. 1, 67–78
|
Abstract |
|
We consider the equation −𝜀2Δu = up −uq in a bounded, smooth domain Ω ⊂ ℝN with homogeneous Dirichlet boundary conditions when either 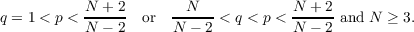 We prove the existence of multiple positive solutions in the case of small diffusion provided the domain Ω is not contractible. |
Keywords
multiple peaks, finite-dimensional reduction, fat diagonal
|
Mathematical Subject Classification 2010
Primary: 35B40, 35J20, 35J55
|
Milestones
Received: 15 April 2011
Revised: 22 June 2011
Accepted: 14 September 2011
Published: 6 May 2012
|
Authors |
| E. Norman Dancer | |
| School of Mathematics and Statistics
F07 University of Sydney NSW 2006 Australia |
|
| Jonathan Hillman | |
| School of Mathematics and Statistics
F07 University of Sydney NSW 2006 Australia |
|
| Angela Pistoia | |
| Dipartimento di Metodi e Modelli
Matematici Università di Roma “La Sapienza” via Antonio Scarpa 16 I-00161 Rome Italy |
|
 |
